 |
|
|
|
|
|
|
|
 |
|
||||||
 |
 |
 |
 |
 |
 |
 |
|
Gradient Covariance
More Tech Stuff:
Indexing Books: Lessons in Language Computations
Constructing a Mandelbrot Set Based Logo with Visual Basic.NET and Fireworks
page 3 of 4
Because I want to use some standard matrix algebra formulas, the above equations can be recast in general form. This introduces the notation 
for constants arranged in matrices. The exercise could be redone for the general case, using the , an exercise left to the reader.
For the arranged in a matrix, i corresponds to the rows and j to the columns. We call this the (coordinate) transformation matrix T:
![T = [a's]](gradient_covariance_files/image042.gif){kind=small}
= 
We will later need to express the 
's in terms of the 
's. This can be done with high school algebra techniques, but matrix techniques were designed to make this easier, especially when problems involve three or more dimensions. We will need to invert T, which we call 
. We’ll need the determinant of the matrix, which is easy for a 2 x 2 matrix:
Then we will use the known formula for inverting 2 x 2 matrices [See also Inverting a Matrix]
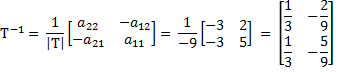
Don’t believe me. The first time I did this I made a subtraction error. The way I found there was an error was testing to see if gets T back for us (the are not from , not the originals).
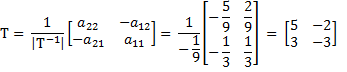
This encapsulates the process of transformations between coordinate systems, which are bidirectional.
Using we can now also write out the in terms of the
By subtracting the second equation from the first you can obtain 
. Then substitute that back in and you get 
, verifying that the transformation equations are consistent.
The Gradient in the New Coordinate System
Our scalar values are expressed as a function F of the
.
Let us substitute in the to get 
Now by taking partial derivatives we can get the gradient components in the new (barred) coordinate system:
Next up: Covariance
continued Gradient Covariance page 4